Variational Autoencoder

生成模型的目标

生成模型（Generative Models）的目的是想学习真实数据分布 $p(x)$， 其中 $X$ 通常是定义在某个（高维）空间 $\mathcal{X}$ 上的数据点。比如一张图像就是一个高维数据点，每个像素对应一个维度。具体来讲生成模型想要解决的问题：考虑一个从真实分布 $p(x)$ 中采样得到的数据集 $ \lbrace{x_1, x_2, \dots, x_n \rbrace}$ ，我们希望从采样得到的数据子集中学习一个分布 $p_\theta(x)$ ，逼近真实分布 $p(x)$。

变分自编码器 Variational Autoencoder

变分自编码器（VAE）作为一种生成模型，依然在现在的机器学习算法占有一席之地。VAE的优化目标推导其实有好几种方式，在开始之前，我想先从最简单的例子开始。

简单假设下存在的问题

考虑对人脸数据集CelebA的建模，我们希望从CelebA数据集中学习到分布 $p_\theta(x)$，然后从 $p_\theta(x)$ 中采样得到新的人脸样本。从流形假设（Manifold Hypothesis）的角度来讲，自然图像数据在高维像素空间中形成一个稠密子集，其内在结构可以用一个低维、非线性流形来近似建模；或者说，图像数据服从一个 嵌入在高维像素空间中低维非线性流形分布 。以CelebA为例，每张图像的数据维度为178x218x3维，RGB图像每一维有256种取值，这个一个非常庞大的高维空间，只有极少数组合才对应一张“真实的人脸”，实际上影响人脸的因素可以抽象为具体几类（比如表情，年龄，肤色，五官轮廓等等）。当然，具体抽象成哪些类别并不是我们关心的问题，我们关心的是高维（图像）数据 $x$ 到低维空间隐变量 $z$（latent variables）的映射关系，通过构建这对映射关系，我们能够实现从 $p(z)$ 中采样，生成新样本 $ \hat{x}$。其实深度学习中不少领域都与该流形假设有关，比如自编码器、表示学习、对抗样本等。

基于上面的想法，一个很自然的想法浮现在脑海中：可以直接构建一个解码器（Decoder），从先验分布 $p(z)$ 中采样，作为Decoder的输入，生成样本并和真实分布中的数据求距离：

$$ \begin{equation} \begin{aligned} p_{\theta}(X) &= \int p_{\theta}(X|z)p(z) dz \\ &= \int \mathcal{N}(X|f(z;\theta), \Sigma) \cdot \mathcal{N}(z|0, I) dz \\ &= \mathbb{E}_{z \sim p(z)} \left[ p_{\theta}(X|z) \right] \\ &\approx \frac{1}{m} \sum_{i=0}^{m} p_{\theta}(X|z_{i}) \end{aligned} \end{equation} $$

其中，$f(z;\theta)$ 是隐变量 $z$ 到样本空间 $ X$ 的映射函数，在这里也就是Decoder，隐变量 $z$ 通常假设为服从均值为 $0$，协方差矩阵为单元矩阵 $I$ 的高斯分布 $\mathcal{N}(z|0, I) $；Decoder生成的样本分布 $p_{\theta}(X|z)$ 的均值，协方差矩阵 $\Sigma$ 一般设为常数。容易发现，我们利用蒙特卡洛采样（Monte Carlo Sampling）从 $p(z)$ 中采样，经过Decoder就可以生成新的样本了，然后计算损失，反向传播优化Decoder了。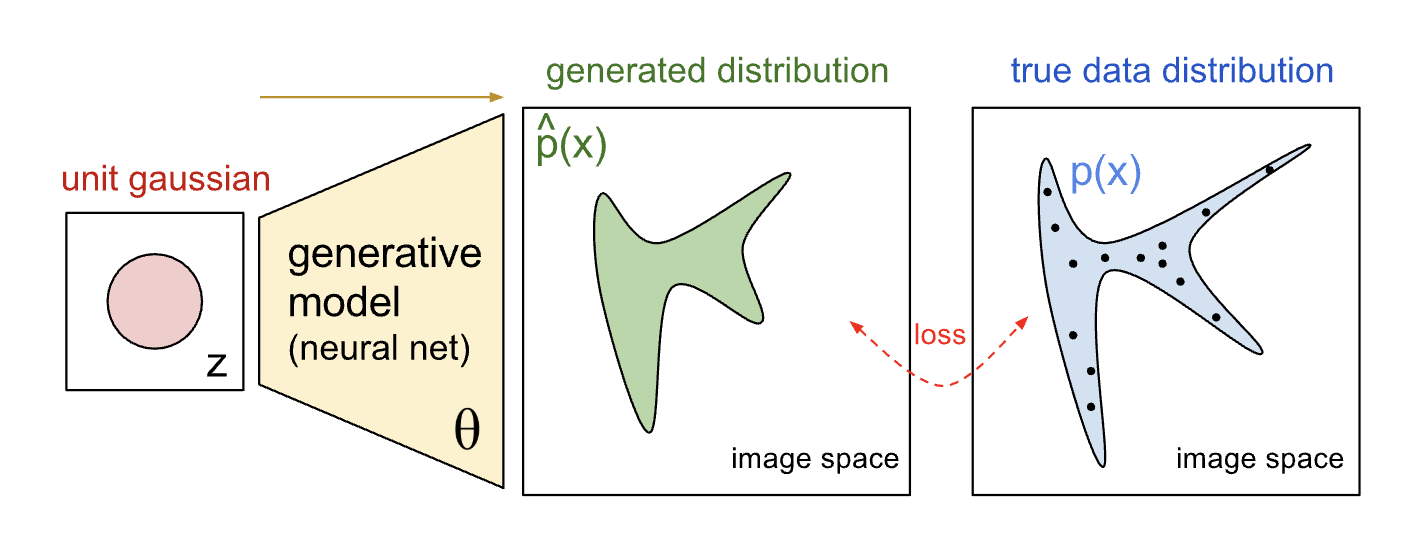

在实际应用中，我们往往只会从 $p(z)$ 中采样一次（在这里，只采样一次其实是有问题的，因为没有构建约束关系，采样出来的大部分 $z$ 都是没有意义的），来计算下目标函数，我们希望最大化 $p_{\theta}(X)$，为了方便计算会取 $log$，也就是最大化 $ log p_{\theta}(X) $ ，设 $ X$ 的维度为 $ K$ ：

$$ \begin{equation} \begin{aligned} \log p_{\theta}(X) &\approx \frac{1}{m} \sum_{i=0}^{m} p_{\theta}(X|z_{i}) \\ &= \frac{1}{m} \sum_{i=0}^{m} \log \left( \frac{1}{(2\pi)^{K/2} |\Sigma|^{1/2}} \exp\left(-\frac{1}{2} (X - f(z_i))^T \Sigma^{-1} (X - f(z_i))\right) \right) \\ &= \frac{1}{m} \sum_{i=0}^{m} \left[ -\frac{K}{2} \log(2\pi) - \frac{1}{2} \log |\Sigma| - \frac{1}{2} (X - f(z_i))^T \Sigma^{-1} (X - f(z_i)) \right] \\ &\propto \frac{1}{m} \sum_{i=0}^{m} - \frac{1}{2} (X - f(z_i))^T \Sigma^{-1} (X - f(z_i)) \\ &\propto \frac{1}{m} \sum_{i=0}^{m} \sum_{k=0}^{K} \frac{\left( x^{(k)} - f(z_i;\theta)^{(k)} \right)^{2}}{\sigma^{(k)}} \\ &\propto \frac{1}{m} \sum_{i=0}^{m} \sum_{k=0}^{K} \left( x^{(k)} - f(z_i;\theta)^{(k)} \right)^{2} \end{aligned} \end{equation} $$

因为我们假设 $p_{\theta}(X|z)$ 的协方差 $\Sigma$ 为常数，因此去掉与Decoder无关的常数后，最后的优化目标等价于生成样本和目标样本的 $ L2 $距离。得到优化目标，可以跑模型看下具体效果了，开始前可以思考下为什么假设 $ p(z) ～ \mathcal{N}(z|0, I) $，这里其实是藏着机器学习中生成模型的一个核心思想“将一组服从标准正态分布的变量通过一个合适的复杂函数映射，可以生成任意维度/任意复杂的分布”。

在CelebA数据集上，我按上述的推导，训练了一个Decoder 20个epoch，以下是损失曲线和生成图像的可视化结果：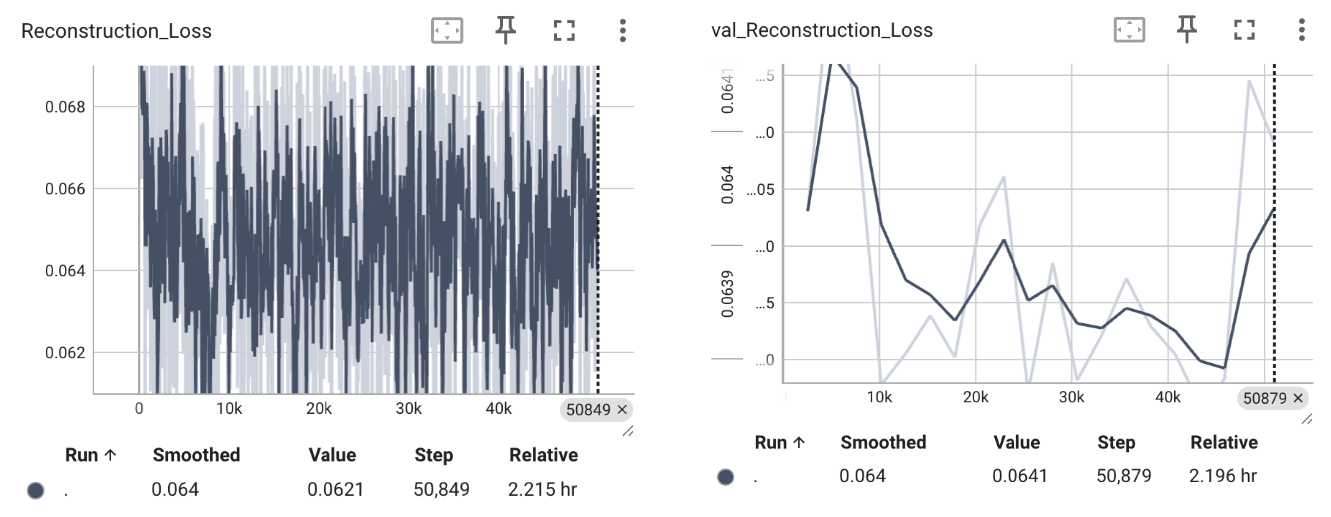

可以看到，首先训练和验证阶段的损失函数，是无法收敛的；至于重建图像，模型训练倾向于生成一张“平均脸”，确切地说，在训练的第一个epoch，采样出来的不同 $z$ 就都倾向于生成“平均脸”了。这是一种在生成模型中很常见的现象：模式崩塌（mode collapse）。思考下为什么会导致这种情况：本质是因为Decoder忽略了输入 $z$ 的多样性，找到了一个局部最优解，即忽略输入$z$ 也能通过输出“平均脸”最小化损失函数（看上图，显然模型在非常早期就陷入了局部最优区域）；核心其实是我们完全没有构建 $ X 和 z$之间的约束关系，因为Decoder是一个确定性的映射，理想情况下其实是希望每个 $z$都能对应一个样本 $x_{i}$，但在这个框架下，显然是做不到的。数据量和模型容量都是有限的，并且实际训练的时候，我们也只对 $z$采样了一次，Decoder并不能学习到这么复杂的映射关系，转而“取巧”学习了“平均脸”的信息。

正文

如果我们能够知道真实的后验分布 $p(z|X)$，似乎就能解决这个问题：

$$ \begin{equation} \begin{aligned} p_{\theta}(x) &= \frac{p_{\theta}(X, z)}{p(z|X)} \\ &= \frac{P_{\theta}(X|z)p(z)}{p(z|X)} \end{aligned} \end{equation} $$

(注意这里可能会有歧义，我用 $p(z|X)$替代了 $p_{\theta}(z|X)$，但最后都会优化掉)。因为 $ p(z) \sim \mathcal{N}(z|0, I) $，而 $p_{\theta}(X|z)$ 就是Decoder所生成的分布，如果知道真实后验分布 $p(z|x)$，那我们也可以直接优化目标函数。但核心 $p(z|x)$ 是untracble的 （当然更严谨一点讲，也可以用hybird MC等方式来逼近，但就不在这里的讨论范畴了）。

于是在VAE中，我们可以用变分贝叶斯，引入一个Encoder，生成 $ q_{\phi}(z|X) \sim \mathcal{N}(z|\mu(X;\phi), \sigma(X;\phi)I)$ 来逼近真实后验分布 $p(z|X)$ （类似地，这里协方差矩阵也为对角矩阵）。重新推导目标函数：

$$ \begin{equation} \begin{aligned} \log p_{\theta}(X) &= \log p_{\theta}(X) \int q_{\phi}(z|X) dz \\ &= \int q_{\phi}(z|X) \log p_{\theta}(X) dz \\ &= \int q_{\phi}(z|X) \log \frac{p_{\theta}(X,z)}{p(z|X)} \\ &= \int q_{\phi}(z|X) \log \frac{p_{\theta}(X,z)}{q_{\phi}(z|X)} \cdot \frac{q_{\phi}(z|X)}{p(z|X)} dz \\ &= \int q_{\phi}(z|X) \log \frac{p_{\theta}(X,z)}{q_{\phi}(z|X)} dz + \int q_{\phi}(z|X) \log \frac{q_{\phi}(z|X)}{p(z|X)} dz \\ &= \mathbb{E}_{q_{\phi}(z|X)} \left[ \log \frac{p_{\theta}(X,z)}{q_{\phi}(z|X)} \right] + D_{\text{KL}}(q_{\phi}(z|X) \| p(z|X)) \\ &\geq \mathbb{E}_{q_{\phi}(z|X)} \left[ \log \frac{p_{\theta}(X,z)}{q_{\phi}(z|X)} \right] \end{aligned} \end{equation} $$

因为真实后验分布 $p(z|X)$ 没有解析解，且KL散度这一项 $ D_{\text{KL}}(q_{\phi}(z|X) | p(z|X)) $ 始终是大于0的，因此目标优化函数可以改为最大化 第一项。在变分贝叶斯方法中，这个损失函数被称为变分下界或证据下界（variational lower bound, or evidence lower bound） ：

$$ \begin{equation} \begin{aligned} \mathbb{E}_{q_{\phi}(z|X)} \left[ \log \frac{p_{\theta}(X,z)}{q_{\phi}(z|X)} \right] &= \log p_{\theta}(X) - D_{\text{KL}}(q_{\phi}(z|X) \| p(z|X)) \end{aligned} \end{equation} $$

不难发现，最大化变分下界 等价于最大化 $p_{\theta}(x)$ 并最小化 $D_{\text{KL}}(q_{\phi}(z|X) | p(z|X))$，这2个目标都恰恰是我们希望优化的。那么来计算下该变分下界的解析解：

$$ \begin{equation} \begin{aligned} \mathbb{E}_{q_{\phi}(z|X)} \left[ \log \frac{p_{\theta}(X,z)}{q_{\phi}(z|X)} \right] &= \mathbb{E}_{q_{\phi}(z|X)} \left[ \log \frac{p_{\theta}(X｜z)p(z)}{q_{\phi}(z|X)} \right] \\ &= \mathbb{E}_{q_{\phi}(z|X)} \left[ \log p_{\theta}(X|z)\right] - D_{\text{KL}}(q_{\phi}(z|X) \| p(z)) \end{aligned} \end{equation} $$

完美，第一项的解析解在前面我们已经算过了，通过MC采样我们可以近似求出其解析解，区别在于隐变量 $z$ 之前是从 $p(z) \sim \mathcal{N}(z|0, I) $ 中采样，而现在是从 $q_{\phi}(z|X) \sim \mathcal{N}(z|\mu(X;\phi), \sigma(X;\phi)I) $ 中采样；而第二项中，2个高斯分布间的KL散度也可以直接算出来解析解：

$$ \begin{equation} \begin{aligned} D_{\text{KL}}\left(\mathcal{N}(\mu_0, \Sigma_0) \parallel \mathcal{N}(\mu_1, \Sigma_1)\right) = \frac{1}{2} \left[ \operatorname{tr}(\Sigma_1^{-1}\Sigma_0) + (\mu_1 - \mu_0)^\top \Sigma_1^{-1}(\mu_1 - \mu_0) - k + \log \frac{\det \Sigma_1}{\det \Sigma_{0}} \right] \end{aligned} \end{equation} $$

最后一步，让我们来计算优化目标最后的解析解。第一项，我们假设 $p_{\theta}(X|z)$ 的协方差为全为 $\frac{1}{2}$ 的对角矩阵；第二项，设隐变量 $z$ 维度为 $d$带入上述KL散度的解析解。优化目标的最终形式可以表示为：

$$ \begin{equation} \begin{aligned} \mathbb{E}_{q_{\phi}(z|X)} \left[ \log \frac{p_{\theta}(X,z)}{q_{\phi}(z|X)} \right] &= \mathbb{E}_{q_{\phi}(z|X)} \left[ \log \frac{p_{\theta}(X｜z)p(z)}{q_{\phi}(z|X)} \right] \\ &= \mathbb{E}_{q_{\phi}(z|X)} \left[ \log p_{\theta}(X|z)\right] - D_{\text{KL}}(q_{\phi}(z|X) \| p(z)) \\ &\propto \frac{1}{m} \sum_{i=0}^{m} \sum_{k=0}^{K} \left( x^{(k)} - f(z_i;\theta)^{(k)} \right)^{2} - \frac{1}{2} \sum_{j=0}^{d} \left( -1 + \mu^{j^{2}}(X;\phi) + \sigma^{j^{2}}(X;\phi) -\log \sigma^{j^{2}}(X;\phi) \right) \\ \end{aligned} \end{equation} $$

好，得到目标损失函数了，可以训练VAE模型看看效果了，注意这里还是只对 $q_{\phi}(z|X) \sim \mathcal{N}(z|\mu(X;\phi), \sigma(X;\phi)I) $ 采样一次，因为我们引入Encoder构建约束关系后，采样出来的隐变量 $z$ 大部分都是有意义的，所以也不太担心会严重的模式坍塌现象了。类似的，在CelebA上，我训练了一个VAE模型，以下是损失曲线和生成图像的可视化结果：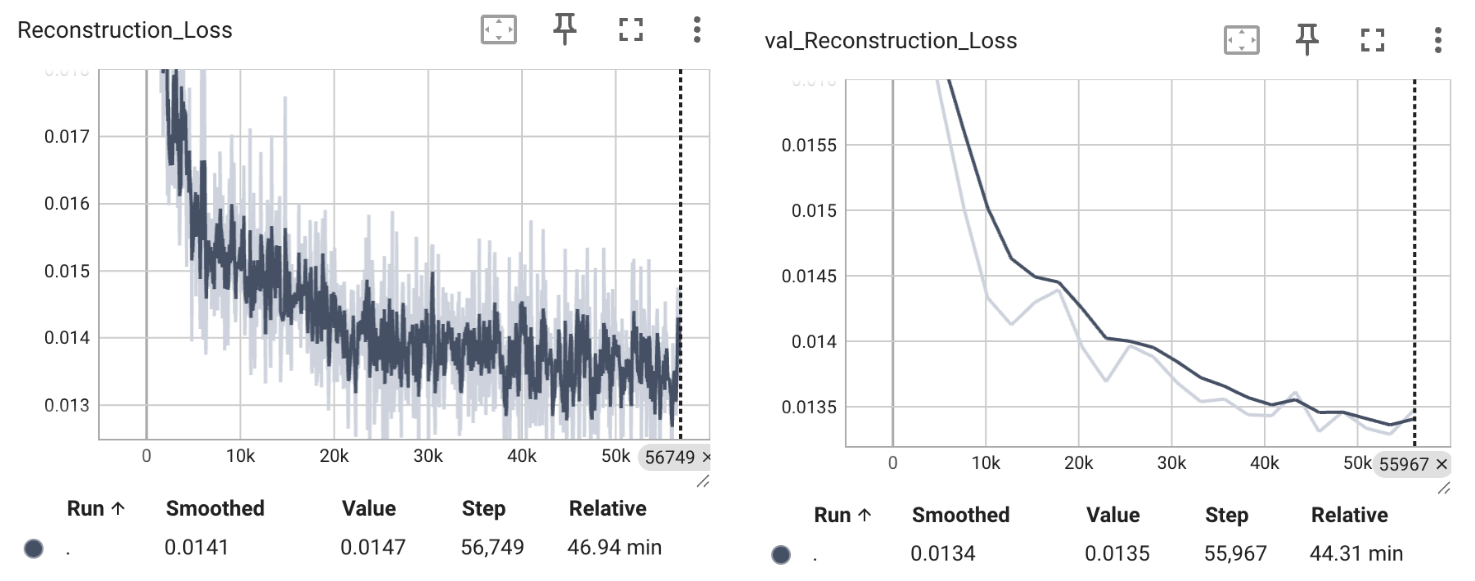

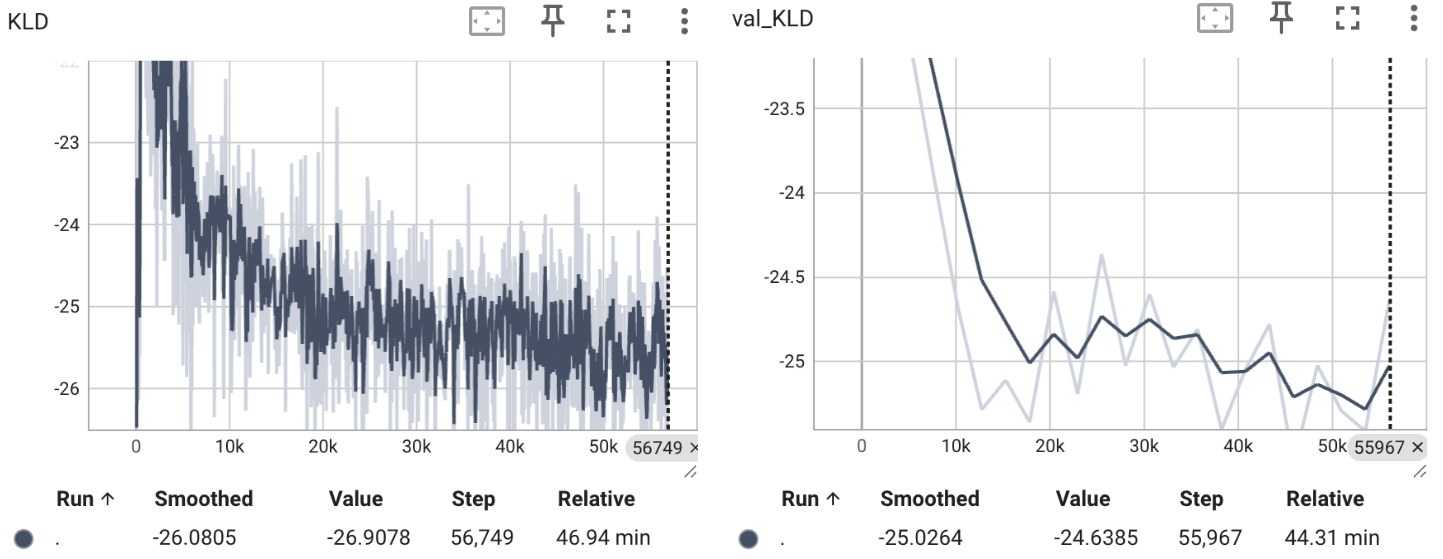
可以发现，无论是第一项的重建损失项还是第二项拟合真实后验分布的 $q_{\phi}(z|X)$ 和先验分布 $p(z)$ 间的KL散度，都是正常收敛的状态。可视化的结果也还不错，至少比较多样，不会崩塌到“平均脸”。但还有一个问题值得注意，因为我们优化的是变分下界，$D_{\text{KL}}(q_{\phi}(z|X) | p(z|X))$ 这一项可能会引入一些误差，但这个误差项又很难直观表现出来，这也是很多后续工作优化/讨论的地方。

其实关于VAE，还有很多值得讨论研究的点。比如最终优化目标的重建损失和KL散度，其实KL散度更像是正则项，重建损失和KL散度之间构成一个trade-off关系：更具体地来说，我们虽然会假设 $p_{\theta}(X|z)$ 的协方差矩阵为常数，但实际采样过程中，并不会再加一个高斯噪声来模拟，而是直接取均值，那如果这里对协方差矩阵的假设为一个与可控常数 $ \beta$ 相关的对角矩阵，最终优化目标可以（不严谨地）等价为以下形式：

$$ \begin{equation} \begin{aligned} \beta \cdot \mathbb{E}_{q_{\phi}(z|X)} \left[ \log p_{\theta}(X|z)\right] - D_{\text{KL}}(q_{\phi}(z|X) \| p(z)) \end{aligned} \end{equation} $$

那就等价于Beta-VAE了，当然Beta-VAE的出发点不同，是将等式重写为KKT条件下的拉格朗日形式。